Part of a series on quantitative models for cause selection.

Introduction

Last time, I wrote about the most likely far future scenarios and how good they would probably be. But my last post wasn’t precise enough, so I’m updating it to present more quantitative evidence.

Particularly for determining the value of existential risk reduction, we need to approximate the probability of various far future scenarios to estimate how good the far future will be.

I’m going to ignore unknowns here–they obviously exist but I don’t know what they’ll look like (you know, because they’re unknowns), so I’ll assume they don’t change significantly the outcome in expectation.

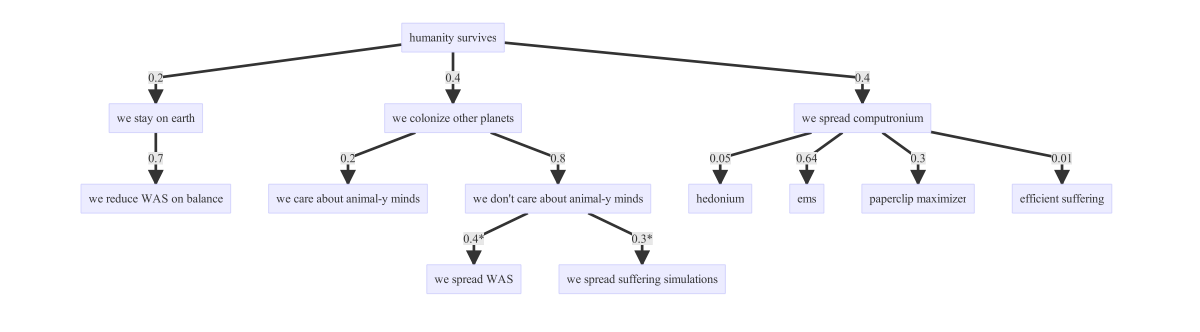
Here are the scenarios I listed before and estimates of their likelihood, conditional on non-extinction:

*not mutually exclusive events

(Kind of hard to read; sorry, but I spent two hours trying to get flowcharts to work so this is gonna have to do. You can see the full-size image here or by clicking on the image.)

I explain my reasoning on how I arrived at these probabilities in my previous post. I didn’t explicitly give my probability estimates, but I explained most of the reasoning that led to the estimates I share here.

Some of the calculations I use make certain controversial assumptions about the moral value of non-human animals or computer simulations. I feel comfortable making these assumptions because I believe they are well-founded. At the same time, I recognize that a lot of people disagree, and if you use your own numbers in these calculations, you might get substantially different results.

Contents

• Introduction
• Contents
• Further justification for given probabilities
• We spread computronium
  • Hedonium Condition
  • Ems Condition
  • Paperclip Condition
  • Efficient Suffering Condition
• We colonize other planets, a.k.a Biological Condition
  • Effect on wild animal suffering
  • Effect on suffering simulations
• We stay on earth
• Table of results
• Notes

Further justification for given probabilities

Let’s estimate the expected utility of each of the far-future outcomes listed above.

We spread computronium

Hedonium Condition

Here I will draw heavily on Bostrom’s Astronomical Waste paper. Originally, I tried to create an independent estimate, but quickly realized I was citing the same sources as Bostrom and doing a worse job. I ultimately decided I might as well work off of his.

Per Bostrom:

• (a) The Virgo Supercluster contains 10¹³ stars.
• (b) If we efficiently built computational infrastructure around a star using plausibly feasible technology, we could perform 10⁴² operations per second.
• (c) A human brain can perform about 10¹⁷ operations per second.

Therefore, a far future supercivilization could support 10³⁸ human-like brains at a time.

Expanding on (b): Bostrom cites Bradbury[^3], claiming we could perform 10⁴² operations per second with a star’s resources, using 10²⁶ watts.

An intergalactic supercivilization might face more limitations of available material than energy output, in which case maximum computation could be lower than 10⁴² operations per second. According to Bradbury, a solar system has about 10²⁶ kg of matter not including the star itself, so if matter is a limiting factor then it’s probably not much more limiting than energy. Of the 10²⁶ watts output by a typical star (according to Bradbury), let’s say we could use 10²⁰ to 10²⁵ as an 80% confidence interval. I made this interval extra wide because we might find limitations on how much energy we can harness, e.g., we may lack enough silicon to build many computers.

I believe the 10⁴² number comes from taking the number of brain operations per watt and multiplying it by a star’s energy output. Next, we divide by the number of brain operations per watt to find the number of brains a star can support. Let’s simplify that by estimating how many watts a brain would need.

A human brain uses about 10¹ watts, but it probably does a lot of unnecessary computation. Chicken brains[^4] are about 1/1000 the mass of human brains (and presumably use linearly less energy) and it seems unlikely that they’re significantly less sentient than humans. If we specifically optimized a brain for experiencing happiness/eudaimonia, we could probably get this down to 10^-2 watts per human-happiness-equivalent brain, and maybe lower.

On (a): A random page on the internet claims that the Virgo Supercluster contains about 10¹⁴ stars. Possibly, we could expand beyond the Virgo Supercluster or something could prevent us from expanding that much, so let’s say our 80% CI on the number of stars we can use is (10<sup>11</sup>, 10<sup>14</sup>).

According to the best source on everything, galaxies’ power output will begin to diminish in about 10¹² years. It takes some amount of time to scale up a civilization to use an entire galactic supercluster’s resources, but that would still take several orders of magnitude lower than 10¹² years so we can safely ignore it. It’s possible that stars could die off faster, so let’s say the 80% CI is 10¹¹ to 10¹².

Our estimate for the number of human-year-equivalents (i.e. QALYs) of the far future is

(accessible stars) * (usable wattage of star) * (brains per watt) * (number of years)

Combining these with the CI’s given above:

accessible stars       = (10<sup>11</sup>, 10<sup>14</sup>)
usable wattage of star = (10<sup>20</sup>, 10<sup>25</sup>)
number of years        = (10<sup>11</sup>, 10<sup>12</sup>)
brains per watt        = 10<sup>2</sup>

If these follow a log-normal distribution then the number of happy life years in the far future follows a log-normal distribution with median¹ 3x10<sup>38</sup> and σ² 4.5 orders of magnitude. This is perhaps too conservative because it assumes we cannot access stars outside the Virgo supercluster.

Ems Condition

An em, short for emulation, is a computer program that emulates a human brain. If we assume that ems don’t evolve toward greater suffering, then they will be about as happy as modern humans–or perhaps somewhat happier since ems presumably will have greater ability to make themselves happier than biological humans do. To calculate the value of this condition, we can use the same numbers as the hedonium condition, except that we can’t fit as many brains per watt because we’re emulating humans, not highly efficient super-happy beings.

One big concern with ems is that selection pressures could cause them to become less happy over time and perhaps turn into paperclip maximizers². But Carl Shulman has argued that happy beings are only slightly less efficient than non-happy beings, so I’m not confident that ems would end up moving in a less happy direction.

Paperclip Condition

Paperclip maximizers might experience consciousness or include conscious components. The critical question here is, do we have reason to expect these conscious components to have net negative lives on balance?

There are a couple of reasons to believe that suffering might dominate in paperclip maximizers:

1. Maximal suffering is more severe than maximal happiness in all the beings we know about.
2. Failure conditions tend to be more severe than success conditions, and if happiness/suffering link to success/failure conditions as they do in sentient animals, then we would expect suffering to be more severe than happiness.

Even considering these, we may find it plausible that happiness could dominate suffering. For example, most humans have net positive lives, even though they’re capable of greater suffering than happiness, simply because they spend more time (mildly) happy than they spend suffering. This might hold true for paperclip maximizers, as well.

But paperclip maximizers probably would look extremely different from animals, so we can’t necessarily expect that they would experience consciousness in the same way (if they’re even conscious at all).

Given how little we know, we can reasonably say that paperclip maximizers in expectation look similar to wild animals in terms of their distribution of happiness and suffering. Perhaps a paperclip maximizer brain experiences between -0.01 and -1 QALYs per watt-year. Then to calculate the expected utility of the paperclip maximizer scenario, we’ll use the same numbers as the previous section but change the number of brains per watt to 10^-1. Then parameters (median, σ²) for the number of suffering life years in the paperclip condition are (6x10<sup>44</sup>, 5.0).

Efficient Suffering Condition

If humanity doesn’t become extinct, then we might end up creating computronium that efficiently fills the universe with suffering. This doesn’t seem all that likely, but I don’t believe it’s astronomically unlikely. For example, someone may (accidentally or intentionally) build a sadistic AI.

If happiness and suffering are symmetric, this condition has the same utility as the hedonium condition, only it’s negative.

We colonize other planets, a.k.a Biological Condition

If we fill the universe with basically humans, then we can still use the same number of stars, but we can support a lot fewer conscious beings per star. We could fairly easily support 10¹⁰ humans per star since we’re already doing that. We might have lots of wild animals or we might not; I’ll estimate this later. Let’s say we have 10¹⁰ to 10¹² humans per solar system and that humans are guaranteed to have net positive lives. So then the utility among humans only (not other animals) is

(accessible stars) * (humans per star) * (number of years)

Let’s say that humans might not be as efficient at spreading across the galaxy as perfect computing machines, so let’s widen the confidence interval on the number of stars occupied.

My 80% CI’s for these are

accessible stars = (10<sup>10</sup>, 10<sup>14</sup>)
humans per star = (10<sup>10</sup>, 10<sup>12</sup>)
number of years  = (10<sup>11</sup>, 10<sup>12</sup>)

Then the 80% CI on the number of happy human life years is (10<sup>34</sup>, 10<sup>37</sup>).

Effect on wild animal suffering

The formula here is about the same, but rather than estimate the number of humans per star we calculate the number of wild animals per star. Drawing from Brian Tomasik’s “How Many Wild Animals Are There?”, I estimate the number of human-equivalent wild animals on earth.

I’ll split this into vertebrates and insects since they look different: there are a lot more insects, but they’re also less sentient in expectation.

Let’s say a star can support between 10¹³ and 10¹⁶ wild vertebrates per star, and the expected utility per wild vertebrate is -0.4 after adjusting for sentience. And maybe a star can support between 10¹⁷ and 10²¹ insects with an adjusted expected utility of -0.04 each. Then the probability distribution of far-future wild vertebrate suffering is parameterized by (4x10<sup>37</sup>, 3.5), and insect suffering is parameterized by (1x10<sup>41</sup>, 4.2).

Effect on suffering simulations

It’s probably simplest to estimate the number of suffering simulations in terms of the number of wild animals. We’re probably not extraordinarily good at creating efficient simulations, or else we’d be in the computronium condition. And we might not expend that many computational resources on creating suffering simulations. So let’s say there are around 0.001 to 1 simulated animal-like minds per wild animal. Then our distribution of negative QALYs created by suffering simulations is parameterized by (4x10<sup>39</sup>, 5.3).

We stay on earth

This is the least important condition so I won’t go into too much detail here. Perhaps we alter wild-animal suffering by 10%, whether we make it better or worse. We can use the previous estimate for the amount of wild-animal suffering on earth and multiply by 10% to get the utility of humans continuing to exist on earth. This number is much smaller than the others so we can ignore it without losing much information.

Table of results

Let’s take the results for each condition and adjust for the probability of that condition occurring. That gives us these results:

Category	exp(μ)	σ2
hedonium	6.3e+46	4.5
paperclip (neg)	4.7e+43	5.0
dolorium (neg)	1.6e+46	4.5
bio humans	2.2e+34	2.7
wild verbetrates (neg)	9.0e+36	3.5
insects (neg)	2.8e+40	4.2
bio simulations (neg)	6.7e+38	5.3

If we use these numbers, the expected value of the far future is determined by the hedonium condition because everything else is less significant. Based on these results, I feel comfortable saying that the far future is probably net positive in expectation.

That said, I have significant uncertainty here. There are a few plausible ways this model could be substantially off:

1. It leaves out other important far-future outcomes.
2. The inputs to one or more of the utility estimates are incorrect by multiple orders of magnitude.
3. I am wrong about the moral value of computer-based minds (especially hedonium).
4. Suffering dominates happiness in a way that my inputs do not account for.

This list is non-exhaustive. But in spite of this model’s possible flaws, I feel more confident in it than my previous non-quantitative attempts assessing the value of preventing human extinction.

Notes