Conventional wisdom says charity cost-effectiveness obeys a power law. To my knowledge, this hypothesis has never been properly tested.1 So I tested it and it turns out to be true.

(Maybe. Cost-effectiveness might also be log-normally distributed.)

  • Cost-effectiveness estimates for global health interventions (from DCP3) fit a power law (a.k.a. Pareto distribution) with \(\alpha = 1.11\). [More]
  • Simulations indicate that the true underlying distribution has a thinner tail than the empirically observed distribution. [More]

Contents

Fitting DCP3 data to a power law

The Disease Control Priorities 3 report (DCP3) provides cost-effectiveness estimates for 93 global health interventions (measured in DALYs per US dollar). I took those 93 interventions and fitted them to a power law.

You can see from this graph that the fitted power law matches the data reasonably well:

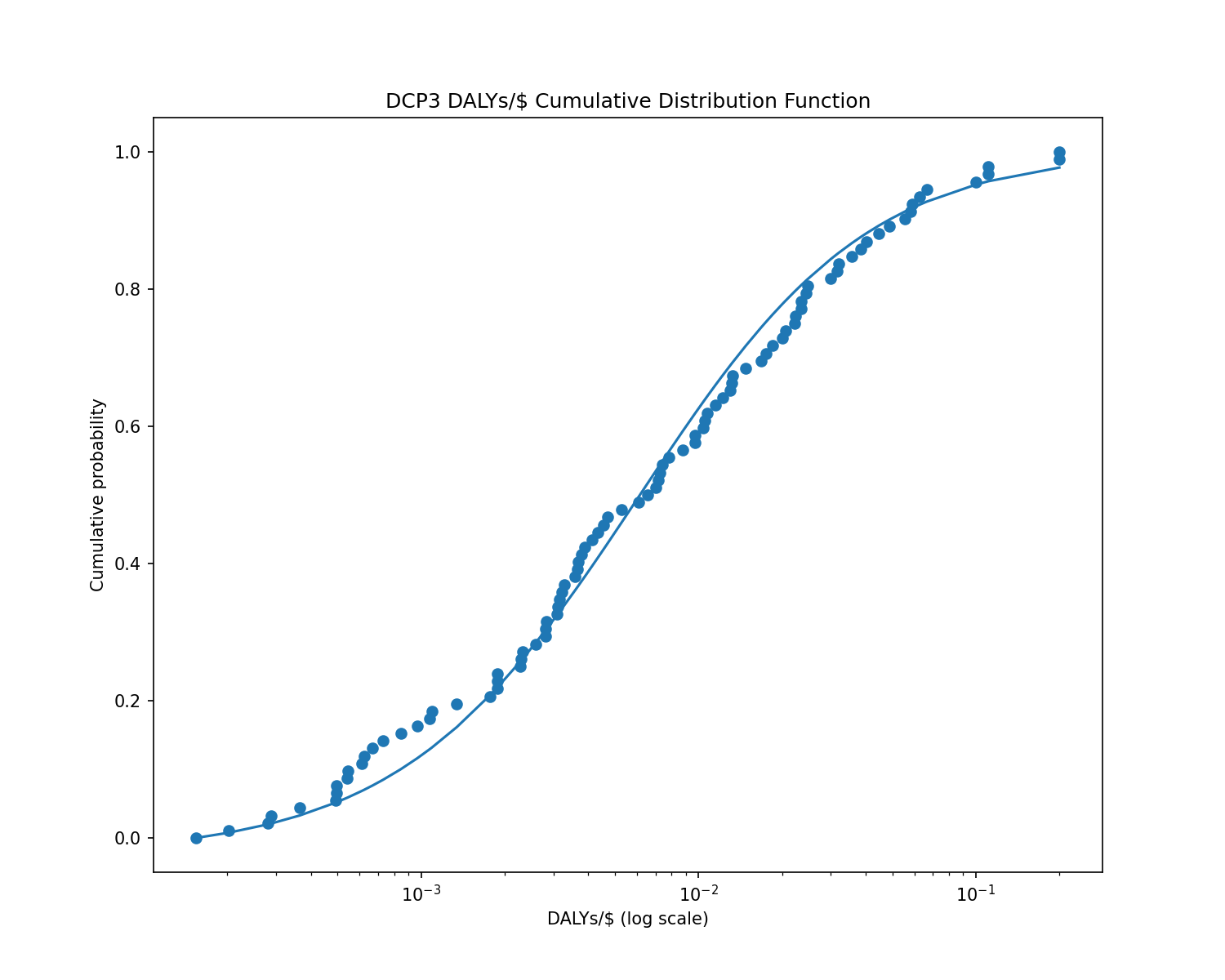
To be precise: the probability of a DCP3 intervention having cost-effectiveness \(x\) is well-approximated by the probability density function \(f(x) = \displaystyle\frac{1.11}{x^{2.11}}\), which is a power law (a.k.a. Pareto distribution) with \(\alpha = 1.11\).

It’s possible to statistically measure whether a curve fits the data using a goodness-of-fit test. There are a number of different goodness-of-fit tests; I used what’s known as the Kolmogorov-Smirnov test2. This test essentially looks at how far away the data points are from where the curve predicts them to be. If many points are far to one side of the curve or the other, that means the curve is a bad fit.

I ran the Kolmogorov-Smirnov test on the DCP3 data, and it determined that a Pareto distribution fit the data well.

The goodness-of-fit test produced a p-value of 0.79 for the null hypothesis that the data follows a Pareto distribution. p = 0.79 means that, if you generated random data from a Pareto distribution, there’s a 79% chance that the random data would look less like a Pareto distribution than the DCP3 data does. That’s good evidence that the DCP3 data is indeed Pareto-distributed or close to it.3

However, the data also fits well to a log-normal distribution.

Pareto and log-normal distributions look similar most of the time. They only noticeably differ in the far right tail—a Pareto distribution has a fatter tail than a log-normal distribution, and this becomes more pronounced the further out you look. But in real-world samples, we usually don’t see enough tail outcomes to distinguish between the two distributions.

DCP3 only includes global health interventions. If we expanded the data to include other types of interventions, we might find a fatter tail, but I’m not aware of any databases that cover a more comprehensive set of cause areas.

(The World Bank has data on education interventions, but adding one cause area at a time feels ad-hoc and it would create gaps in the distribution.)

Does estimation error bias the result?

Yes—it causes you to underestimate the true value of \(\alpha\).

(Recall that the alpha (\(\alpha\)) parameter determines the fatness of the tail—lower alpha means fatter tail. So estimate error makes the tail look fatter than it really is.)

There’s a difference between cost-effectiveness and estimated cost-effectiveness. Perhaps estimation error follows a power law, but the true underlying cost-effectiveness numbers don’t. And even if they do, our cost-effectiveness estimates might produce a bias in the shape of the fitted distribution.

I tested this by generating random Pareto-distributed4 data to represent true cost-effectiveness, and then multiplying by a random noise variable to represent estimation error. I generated the noise as a log-normally-distributed random variable centered at 1 with \(\sigma = 0.5\)5 (colloquially, that means you can expect the estimate to be off by 50%).

I generated 10,000 random samples6 at various values of alpha, applied some estimation error, and then fit the resulting estimates to a Pareto distribution. The results showed strong goodness of fit, but the estimated alphas did not match the true alphas:

true alpha 0.8  -->  0.73 estimated alpha (goodness-of-fit: p = 0.3)
true alpha 1.0  -->  0.89 estimated alpha (goodness-of-fit: p = 0.08)
true alpha 1.2  -->  1.07 estimated alpha (goodness-of-fit: p = 0.4)
true alpha 1.4  -->  1.22 estimated alpha (goodness-of-fit: p = 0.5)
true alpha 1.8  -->  1.54 estimated alpha (goodness-of-fit: p = 0.1)

To determine the variance of the bias, I generated 93 random samples at a true alpha of 1.1 (to match the DCP3 data) and fitted a Pareto curve to the samples. I repeated this process 10,000 times.

Across all generations, the average estimated alpha was 1.06 with a standard deviation of 0.27. That’s a small bias—only 0.04—but it’s highly statistically significant (t-stat = –15, p = 07).

A true alpha of 1.15 produces a mean estimate of 1.11, which equals the alpha of the DCP3 cost-effectiveness data. So if the DCP3 estimates have a 50% error (\(\sigma = 0.5\)), then the true alpha parameter is more like 1.15.

Increasing the estimate error greatly increases the bias. When I changed the error (the \(\sigma\) parameter) from 50% to 100%, the bias became concerningly large, and it gets larger for higher values of alpha:

true alpha 0.8  -->  0.65 mean estimated alpha
true alpha 1.0  -->  0.78 mean estimated alpha
true alpha 1.2  -->  0.87 mean estimated alpha
true alpha 1.4  -->  0.96 mean estimated alpha
true alpha 1.6  -->  1.03 mean estimated alpha
true alpha 1.8  -->  1.11 mean estimated alpha

If the DCP3 samples have a 100% error then the true alpha is 1.8—much higher than the estimated value of 1.11.

In addition, at 100% error with 10,000 samples, the estimates no longer fit a Pareto distribution well—the p-value of the goodness-of-fit test ranged from 0.005 to <0.00001 depending on the true alpha value.8

Curiously, decreasing the estimate error flipped the bias from negative to positive. When I reduced the simulation’s estimate error to 20%, a true alpha of 1.1 produced a mean estimated alpha of 1.14 (standard deviation 0.31, t-stat = 13, p = 07). A 20% error produced a positive bias across a range of alpha values—the estimated alpha was always a bit higher than the true alpha.

Future work I would like to see

  1. A comprehensive DCP3-esque list of cost-effectiveness estimates for every conceivable intervention, not just global health. (That’s probably never going to happen but it would be nice.)
  2. More data on the outer tail of cost-effectiveness estimates, to better identify whether the distribution looks more Pareto or more log-normal.

Source code and data

Source code is available on GitHub. Cost-effectiveness estimates are extracted from DCP3’s Annex 7A; I’ve reproduced the numbers here in a more convenient format.

Notes

  1. The closest I could find was Stijn on the EA Forum, who plotted a subset of the Disease Control Priorities data on a log-log plot and fit the points to a power law distribution, but did not statistically test whether a power law represented the data well. ↩

  2. Some details on goodness-of-fit tests:

    Kolmogorov-Smirnov is the standard test, but it depends on the assumption that you know the true parameter values. If you estimate the parameters from the sample (as I did), then it can overestimate fit quality.

    A recent paper by Suarez-Espinoza et al. (2018)9 devises a goodness-of-fit test for the Pareto distribution that does not depend on knowing parameter values. I implemented the test but did not find it to be more reliable than Kolmogorov-Smirnov—for example, it reported a very strong fit when I generated random data from a log-normal distribution. ↩

  3. A high p-value is not always evidence in favor of the null hypothesis. It’s only evidence if you expect that, if the null hypothesis is false, then you will get a low p-value. But that’s true in this case.

    (I’ve previously complained about how scientific papers often treat p > 0.05 as evidence in favor of the null hypothesis, even when you’d expect to see p > 0.05 regardless of whether the null hypothesis was true or false—for example, if their study was underpowered.)

    If the data did not fit a Pareto distribution then we’d expect to see a much smaller p-value. For example, a goodness-of-fit test for a normal distribution gives p < 0.000001, and a gamma distribution gives p = 0.08. A log-normal distribution gives p = 0.96, so we can’t tell whether the data is Pareto or log-normal, but it’s unlikely to be normal or gamma. ↩

  4. Actually I used a Lomax distribution, which is the same as a Pareto distribution except that the lowest possible value is 0 instead of 1. ↩

  5. The \(\sigma\) parameter is the standard deviation of the logarithm of the random variable. ↩

  6. In practice we will never have 10,000 distinct cost-effectiveness estimates. But when testing goodness-of-fit, it’s useful to generate many samples because a large data set is hard to overfit. ↩

  7. As in, the p-value is so small that my computer rounds it off to zero. ↩ ↩2

  8. Perhaps that’s evidence that the DCP3 estimates have less than a 100% error, since they do fit a Pareto distribution well? That would be convenient if true.

    But it’s easy to get a good fit if we reduce the sample size to 93. When I generated 93 samples with 100% error, I got a p-value greater than 0.5 most of the time. ↩

  9. Suárez-Espinosa, J., Villasenor-Alva, J. A., Hurtado-Jaramillo, A., & Pérez-Rodríguez, P. (2018). A goodness of fit test for the Pareto distribution. ↩