If you’re losing weight, does lifting weights reduce how much muscle you lose? Is it possible to entirely prevent muscle loss (or even gain muscle)?

Murphy & Koehler (2021)¹ did a meta-analysis on this question. They collected experiments where the experimental groups did resistance training while eating at an energy deficit (RT+ED), and the control groups did resistance training while eating a normal amount of food (RT+CON).

They found a strong association between change in lean mass and the magnitude of the energy deficit (slope = –0.325, p = 0.001). The meta-analysis predicts that you can eat at a deficit of 500 calories per day without losing any lean mass, but you will lose mass at a larger deficit.

(The meta-analysis also reported that participants gained strength in almost every study, even with larger calorie deficits. That’s useful to know, but I will focus on lean mass for this post.)

I should mention that what we actually care about is muscle loss, not lean mass loss. Lean mass includes anything that isn’t fat—muscle fibers, organs, glycogen, etc. Muscle mass is harder to measure. We don’t know what happened to study participants’ muscle, only their total lean mass.

Let’s set that aside and assume lean mass is a useful proxy for muscle mass.

The authors showed a plot of every individual study’s experimental group (RT+ED) and control group (RT+CON), along with a regression line predicting lean mass change as a function of energy deficit:²

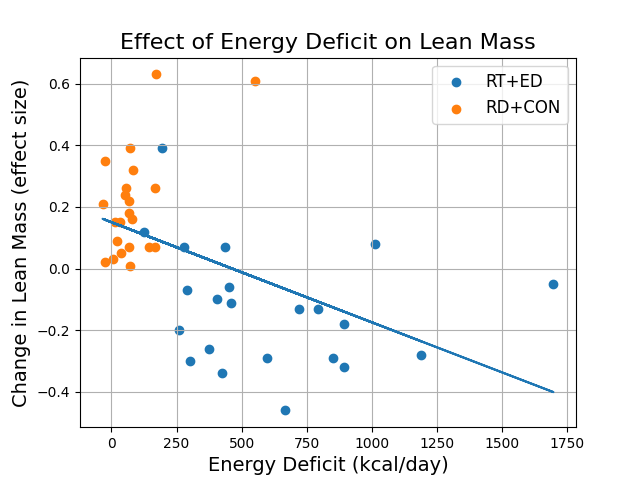
But…does this regression line look a little odd to you?

Where are the RT+CON points, and where are the RT+ED points, relative to the regression line?

In particular, look at all the data points from experimental groups where participants had energy deficits of under 500 calories. Almost all of them lost lean mass on average (recall that each individual point represents the average result from one study); only four gained lean mass.

The slope of the regression line is almost entirely driven by the difference between the experimental and control groups.

What happens if we calculate a regression using only the experimental groups? Did groups with a bigger calorie deficit lose more lean mass?

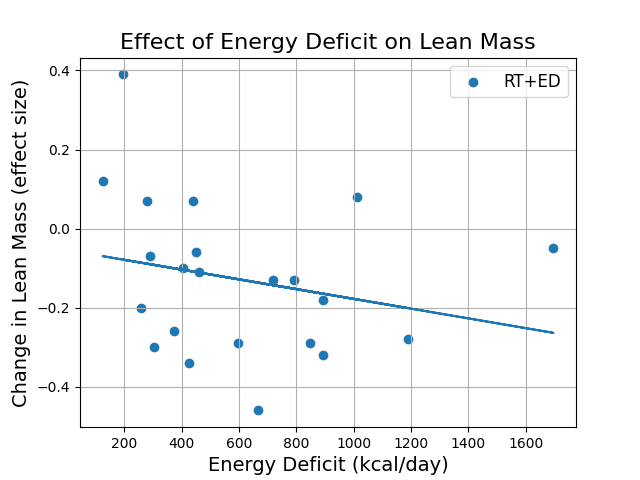
Now the regression has a slope of only –0.123 (p = 0.28), and it predicts that any deficit will cause at least a small loss in lean mass.

So, among study groups where participants ate at a calorie deficit, it does appear that they lost lean mass on average. But there is not a clear relationship between the size of the deficit and the amount of lean mass lost.

In theory, it makes sense that when you have a larger calorie deficit, it should be harder for your body to preserve muscle. But the evidence from this meta-analysis doesn’t really support the theory. (It doesn’t contradict it, either. It just doesn’t say much either way.)

Murphy & Koehler (2021)’s original regression had a slope of –0.325. If that’s the true slope, then it’s unlikely that the experimental-only regression would have the much shallower slope of –0.123 (p = 0.07, likelihood ratio 5.2³).

The conclusions I drew from this meta-analysis:

• Eating at a deficit might cause me to lose muscle, or it might not, who knows.
• In theory, I expect there is some calorie deficit above which I start to lose muscle, but this meta-analysis doesn’t tell me what that number is.

Appendix: What else does this data tell us?

Looking at the experimental-only regression, how much evidence is this for or against the hypothesis that a larger calorie deficit causes more lean mass loss?

The experimental-only regression has slope –0.123 with standard error 0.111. The slope is still negative, which is consistent with the hypothesis, but it’s not strongly negative—only about one standard error away from zero.

The hypothesis predicts a positive intercept: it should be possible to gain muscle while maintaining weight. The experimental-only regression has a negative intercept (–0.054), but it is less than one standard error away from zero (the intercept’s standard error is 0.079). This is weak evidence against the hypothesis.

Source code is available on GitHub.

Notes