Summary

Previously, we talked about how much leverage altruists should use. We looked at estimates of optimal leverage based on future projected returns, but this required making certain assumptions about how asset prices behave.

In many ways, theoretical asset pricing models do not reflect how investments behave in practice. These models may overestimate how much leverage to use. We can learn something about the extent of this overestimation by backtesting leveraged portfolios on historical price data.

In the backtests I performed, theoretically-optimal leverage according to the Samuelson share usually did not differ much from empirically optimal leverage according to backtests. However, the Samuelson share overestimated optimal leverage more often than it underestimated, and following the Samuelson share would have occasionally resulted in bankruptcy.

After performing this analysis, I am now somewhat more confident that it makes sense for altruists to apply substantial leverage to their altruistic portfolios, although probably less than the Samuelson share. However, investors should ensure they understand what that entails—in backtests, optimally-leveraged portfolios usually encountered >90% drawdowns at some points.

Disclaimer: This should not be taken as investment advice. Any given portfolio results are hypothetical and do not represent returns achieved by an actual investor.

Contents

• Summary
• Contents
• Introduction
• Methodology
  • Asset classes
  • Asset class time horizons
  • Asset class costs
• Results
  • Comparing Samuelson share to optimal leverage
    • Some sample portfolios
    • Commentary
  • Effects of under- and over-estimating optimal leverage
    • On risk aversion
    • Some sample portfolios
  • Rebalance timing luck
  • Path dependence
  • How does ex-ante optimal leverage compare to ex-post?
    • Some sample portfolios
    • Commentary
• Conclusions
• Appendix
  • Appendix A: More sample portfolios
  • Appendix B: More over- or under-leveraged sample portfolios
  • Appendix C: More ex-ante optimal leverage portfolios
• Notes

Introduction

When I last wrote about how much leverage altruists might use, I considered a number of caveats that make leverage look less appealing than theoretical models suggest.

These caveats included:

• Mean reversion
• Left skew of investment returns
• Unpredictability of future returns
• Cost of leverage
• Transaction costs
• Taxes
• Portfolios can’t be adjusted continuously

(The original essay explained these caveats in more detail.)

For some of these, we can learn how much they matter by running backtests on historical data. Backtests can only tell us so much about what to expect from future performance, but they can tell us a lot about how to deal with some of these caveats:

• If mean reversion or left skew reduce the value of leverage, this will show up in backtests.
• While theoretical models of leverage generally assume continuous rebalancing, backtests can use a more practical rebalancing schedule (such as monthly).

For some other caveats, backtests don’t definitively tell us how much they matter, but they can help:

• We can estimate costs of leverage, transaction costs, and taxes and subtract them from historical returns.
• Backtests obviously cannot resolve the unpredictability of future return, but they can tell us how a portfolio would have performed if we had mis-estimated future returns or volatility.

Methodology

I performed backtests using publicly-available data from the Ken French data library, the AQR data sets¹, and government bond return series from Laurens Swinkels².

The backtests built in these assumptions:

• The investor has logarithmic utility. This is probably not true for most self-interested investors, but it may apply for altruistic investors. I discuss this in more detail here. In this essay, I will primarily assume logarithmic utility because it appears reasonable and it makes the results easier to reason about.
• Portfolios are rebalanced, and leverage is adjusted, on a monthly basis.
• The investor does not pay taxes.
• The investor can borrow at an interest rate pegged to the risk-free rate (RF). I tested both with interest equal to RF and RF + 1%. Theoretical models generally assume leverage costs the risk-free rate, and some institutional investors may be able to get rates close to RF, while smaller investors generally have to pay more like RF + 1%.
• Asset classes have varying costs depending on their liquidity, trading frequency, or how much investment managers tend to charge for them.

Asset classes

The simulated portfolios in this essay use various combinations of these six asset classes.

1. US stocks: A total market index including all US stocks.
2. International stocks: A total market index including all stocks in all countries other than the United States.
3. Bonds: US 10-year Treasury bonds.
4. Commodities: A passive commodity futures strategy that follows the methodology described in Levine et al. (2016), Commodities for the Long Run, using the associated data set.
5. US value/momentum: A strategy that buys the top decile of value stocks ranked by cash flow to price (CF/P) and the top decile of momentum stocks ranked by 12-2 momentum, allocating 50% to each of the two sub-strategies. I use CF/P as the value metric rather than the more typical book to price or earnings to price because cash flow is less subject to accounting details than book value or earnings. I made this choice before looking at any performance results. For more details on methodology, see Ken French’s descriptions: value, momentum.
6. TSMOM: Time series momentum, also known as managed futures—a strategy that I identified as particularly promising in my original essay on leverage for altruists³. The details of the methodology are described by Hurst et al. (2013), Demystifying Managed Futures. Hypothetical historical performance was calculated using the associated data set.

Asset class time horizons

Some data sources cover shorter time periods than others. When running a backtest that combined multiple asset classes, I used the longest possible time horizon for which all asset classes have data.

The asset classes have data available starting in the following years:

Asset Class	Year
US stocks	1926
international stocks	1990
bonds	1947
commodities	1877
US value/momentum	1952
TSMOM	1985

Each backtest ends in 2018. The exact end month can vary, but this has only a small effect on the results.

Asset class costs

I assumed the following costs for each asset class. These include both fees and transaction costs.

Asset Class	Cost
US stocks	0%
international stocks	0%
bonds	0%
commodities	1%
US value/momentum	2%
TSMOM	5%

Stock index funds rarely trade so they have near zero trading costs, and many fund providers offer mutual funds and ETFs for extremely low fees.

Bond funds have to trade more often as bonds reach maturity and have to roll over, but the Treasury bond market is highly liquid, so this incurs minimal trading costs.

Commodity index funds must regularly trade old futures contracts for new ones, and generally charge higher management fees than stock or bond funds. I don’t have a great sense of how much these cost, so I assumed 1%. This probably underestimates the true cost, but this doesn’t matter much for our purposes.

Frazzini et al. (2013)⁴ found a real-world trading cost of 2.07% for a global value/momentum portfolio run from 1998 to 2011, and an estimated 1.37% trading cost for the same portfolio back to 1926. Furthermore, a value/momentum portfolio with cost-reducing optimizations cost only 1.11% with no reduction in gross return (gross return actually slightly increased, but this was probably due to noise). This analysis may overestimate trading costs relative to my simulated portfolios because it uses long-short strategies while I use long-only; but it definitely underestimates total costs in that it does not include fund fees. Concentrated value/momentum funds exist that cost as little as 0.6%, or investors can manage their own portfolios at the expense of more time spent. Quantitative value and momentum strategies require relatively little effort to trade manually—less than five hours per year⁵.

I have a lot of uncertainty about how much TSMOM costs. Such strategies are usually run by hedge funds that charge 2% fee plus 20% carry, which equates to about a 6% flat fee, but it’s possible to find cheaper implementations. The strategy also incurs substantial transaction costs. Hurst et al. (2013)⁶ estimate them at 1-4% depending on implementation details. A 5% all-in cost falls on the low end of the plausible cost range, but does seem achievable by investors who seek out low-fee, cost-conscious funds.

AXS Chesapeake Strategy Mutual Fund (EQCHX), a real-world fund that follows a strategy similar to TSMOM, provides performance data net of fees over the period 1988 to 2020. (Disclaimer: At the time of this writing, I have money invested in this fund.) If we compare these net returns to the gross returns of the AQR TSMOM portfolio and apply leverage so they have equal variance, we see that EQCHX returned 6-7% less over the sample period. This suggests an all-in cost of 6-7%, although presumably part of this difference in return happened due to implementation differences (the two return series are only correlated with r=0.53).

Results

Comparing Samuelson share to optimal leverage

The Samuelson share (a term I adopted from Lifecycle Investing by Ian Ayres and Barry Nalebuff) indicates how much leverage an investor should theoretically use. The Samuelson share for an investor with logarithmic utility of money is given by

\begin{align} \displaystyle\frac{\mu - R}{\sigma^2} \end{align}

where \(\mu\) is the expected return of the investor’s portfolio, \(R\) is the cost of leverage, and \(\sigma\) is the standard deviation. This formula changes for investors with non-logarithmic utility, but for this essay, I will assume utility is logarithmic. This serves to simplify the analysis, and it seems like a reasonable best guess for how altruists’ utility functions behave.

(Ayres and Nalebuff have a Samuelson share calculator on their website.)

For this analysis, I performed a series of backtests on a variety of portfolios and time horizons. For each portfolio, I first found the return and standard deviation of the portfolio. I used these two numbers to calculate the theoretically-optimal Samuelson share. Then I re-ran the backtest using varying amounts of leverage to find the level that maximized geometric return, which is equivalent to maximizing utility for a logarithmic utility function. I refer to this as “empirically optimal leverage” in the sense that it maximized geometric return over the sample. This does not say anything about its optimality out of sample.

Note that this calculation of the Samuelson share requires perfect foresight—it assumes we know the return and standard deviation over the whole period, which we obviously cannot know in advance. So the Samuelson share does not represent how much leverage we would have thought to use if we had invested over the period. Instead, it represents the theoretically-optimal leverage according to the standard model of how asset prices operate. The point of this analysis is to tell us how historical performance differed from what the theoretical model predicts.

While this analysis looks at past returns, this is not to suggest that future returns will look the same. While we cannot extrapolate returns from these backtests, we can extrapolate knowledge about how well theoretical models predict optimal leverage, insofar as we expect asset prices to behave similarly in the future to how they have in the past (in the shapes of their distributions, not in their returns).

Some sample portfolios

These tables show statistics for simulated portfolios taken 1952-2018, including US stocks, bonds, and commodities. I assume leverage costs RF + 1%, and take the costs for each asset class given in Asset class costs.

Columns are defined as follows:

• Lev: Empirically optimal leverage.
• Sam: Theoretically optimal Samuelson share, calculated using the return, risk-free rate, and standard deviation over the sample period.
• Sharpe: Sharpe ratio, or risk-adjusted return, calculated as \(\frac{\mu - RF}{\sigma}\).
• CAGR: Compound annual growth rate, i.e., geometric return.
• Stdev: Annualized standard deviation of monthly returns.
• MaxDD: Maximum drawdown experienced over the sample period.

Table 1: Summary statistics, 1952-2018

	Lev	Sharpe	CAGR	Stdev	MaxDD
US stocks	2.66	0.27	15.1	39.0	93%
bonds	1.32	0.15	5.8	9.8	25%
commodities	1.34	0.15	7.0	17.9	68%
US val/mom	2.72	0.44	28.8	53.7	96%
60% stock, 40% bond	4.29	0.26	15.3	40.6	93%
60% val/mom, 40% bond	6.63	0.41	27.7	55.2	98%
40% stock, 40% bond, 20% com	5.46	0.27	15.8	40.4	90%
40% val/mom, 40% bond, 20% com	5.89	0.43	28.5	53.4	97%

Table 2: Optimal leverage and Samuelson share, 1952-2018

	Lev	Sam	Lev-Sam
US stocks	2.66	2.57	0.09
bonds	1.32	0.82	0.5
commodities	1.34	0.84	0.5
US val/mom	2.72	3.11	-0.39
60% stock, 40% bond	4.29	4.24	0.05
60% val/mom, 40% bond	6.63	7.59	-0.96
40% US stock, 40% bond, 20% com	5.46	5.72	-0.26
40% val/mom, 40% bond, 20% com	5.89	7.19	-1.3

The following tables give summary statistics for simulated portfolios taken 1985-2018, including time-series momentum (TSMOM). In my previous essay on leverage for altruists, I presented two key potentially-market-beating strategies: value/momentum and managed futures (also known as time series momentum (TSMOM)³). We would like to see how these strategies hypothetically would have performed with optimal leverage, and how optimal leverage compares to Samuelson share over the sample period. Note that the methodologies used here do not perfectly match the methodologies I used to derive hypothetical returns in my previous essay, so the numbers will differ somewhat.

These results cover a shorter time horizon, so they tell us less about how these strategies might have performed in various economic regimes.

Table 3: Summary statistics, 1985-2018

	Lev	Sharpe	CAGR	Stdev	MaxDD
US stocks	2.75	0.31	16.7	41.4	93%
US val/mom	2.40	0.38	22.0	47.3	92%
TSMOM	5.91	0.43	35.2	72.2	95%
50% val/mom, 50% TSMOM	4.38	0.68	39.0	50.9	89%

Table 4: Optimal leverage and Samuelson share, 1985-2018

	Lev	Sam	Lev-Sam
US stocks	2.75	2.93	-0.18
US val/mom	2.40	2.67	-0.27
TSMOM	5.91	5.34	0.57
50% val/mom, 50% TSMOM	4.38	7.33	-2.95

Finally, let’s look at the results for US stocks 1927-2018, a period that includes the Great Depression.

Table 5: Summary statistics, 1927-2018

	Lev	Sharpe	CAGR	Stdev	MaxDD
US stocks	1.91	0.23	11.8	35.2	98%

Table 6: Optimal leverage and Samuelson share, 1927-2018

	Lev	Sam	Lev-Sam
US stocks	1.91	1.60	0.31

I present more hypothetical portfolios in Appendix A, including ones constructed using international equities.

I also tested all of the above portfolios with the assumptions that no asset classes have fees and leverage only costs as much as the risk-free rate. Samuelson share and optimal leverage were both uniformly lower. Removing asset class fees appeared to slightly reduce the difference between Samuelson share and optimal leverage, but reducing the cost of leverage did not appear to matter.

Commentary

First, how does Samuelson share compare to optimal leverage?

I do not believe we can make any statistically significant claims from this backtest. The above results only include five asset classes, which means no matter how many portfolios we construct, we only have five independent data points⁷. And in fact, not all of the asset classes are independent—US stocks and US val/mom, for example, are positively correlated. We would like to know whether there exists a statistically significant difference between optimal leverage and the Samuelson share, but we can’t know that. The best we can do is make some general observations.

For most hypothetical portfolios, Samuelson share did a moderately good job of approximating optimal leverage. Based on this sample, the Samuelson share appears about equally likely to over- or under-estimate optimal leverage. However, it sometimes overestimated leverage by a large margin, such as for the “50% US val/mom, 50% TSMOM” portfolio. As we will discuss in the next section, overestimating leverage can lead to catastrophic outcomes. It appears that using the Samuelson share to determine optimal leverage (even with perfect foresight) has a non-trivial chance of producing a portfolio that will lose greater than 100% of its value in a bad market crash.

On the other hand, Samuelson share does a better job of approximating optimal leverage than I expected. The Samuelson share embeds assumptions that market returns follow a normal distribution and that each period is independent. In reality, the returns distribution show a left skew, and prices tend to mean revert. But, at least based on this limited sample, it does not appear that the Samuelson share consistently overestimates optimal leverage, although it does overestimate sometimes. In my previous essay on leverage, I suggested that investors could use half as much leverage as the Samuelson share suggests, an idea taken from MacLean et al. (2010), Good and bad properties of the Kelly criterion. But this backtest seems to suggest that this rule of thumb may be too conservative. Of course, this backtest does not tell us what to expect from future returns, but it does eliminate certain classes of concerns, such as the left skew of investment returns (unless we expect future returns to have a significantly stronger left skew than past returns did, which I find implausible).

Next, observe that all optimally-leveraged portfolios (except bonds) experienced large drawdowns, usually exceeding 90%. (Leveraged US equities would have experienced a 98% drawdown during the Great Depression!)

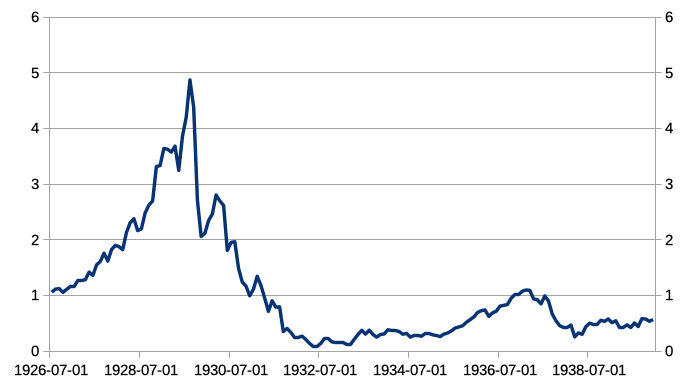
This chart shows a zoomed-in view of optimally-leveraged US stocks’ performance during the Great Depression, with the price on 1926-07-01 (the first day of the sample) normalized to $1:

In the global financial crisis of 2008, this portfolio would have lost over 75% of its value:

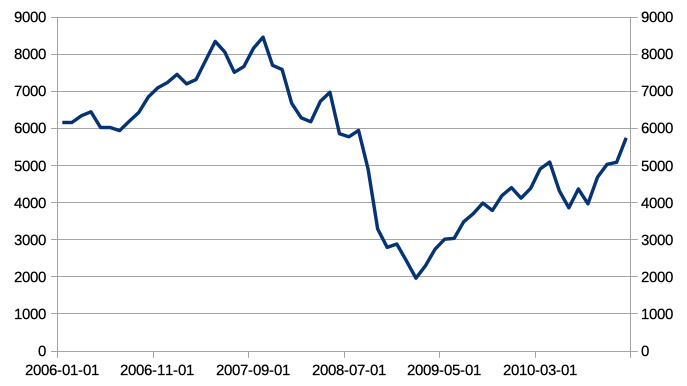
Using optimal leverage according to the 1952-2018 backtest (instead of 1927-2018) would have produced an even larger drawdown in 2008.

Effects of under- and over-estimating optimal leverage

As discussed previously, we can only know the optimal Samuelson share in hindsight. When looking forward, we can only try our best to estimate future expected return and standard deviation. What happens if we get it wrong?

We can learn the impact of using the wrong amount of leverage by looking at how historical portfolios would have performed with too little or too much leverage. For this analysis, I calculate optimal leverage for each portfolio, then find what would have happened with 50 percentage points too little or too much leverage. That is, if optimal leverage was (say) 200%, what would have happened if we had used 150% or 250% instead?

In most cases, using too much or too little leverage had a symmetric effect on (geometric) return. For example, for US stocks 1927-2018, optimal leverage equaled 1.91, which gave an 11.8% return. Using 1.41 or 2.41 leverage resulted in a 11.2% return, with standard deviations of 26% and 45%, respectively. So someone with logarithmic utility is indifferent between these options, and someone with sub-logarithmic utility much prefers the option with too little leverage because it provides equal return with far less risk.

In some cases, the over-leveraged portfolio would have gone bust, which, according to a logarithmic utility function, produces \(-\infty\) utility. Thus, all else equal, even a logarithmic utility function would prefer to undershoot optimal leverage than to overshoot it⁸.

On risk aversion

For US equities 1927-2018, the over-leveraged and under-leveraged portfolios both ended up at the same place, but they took different routes to get there:

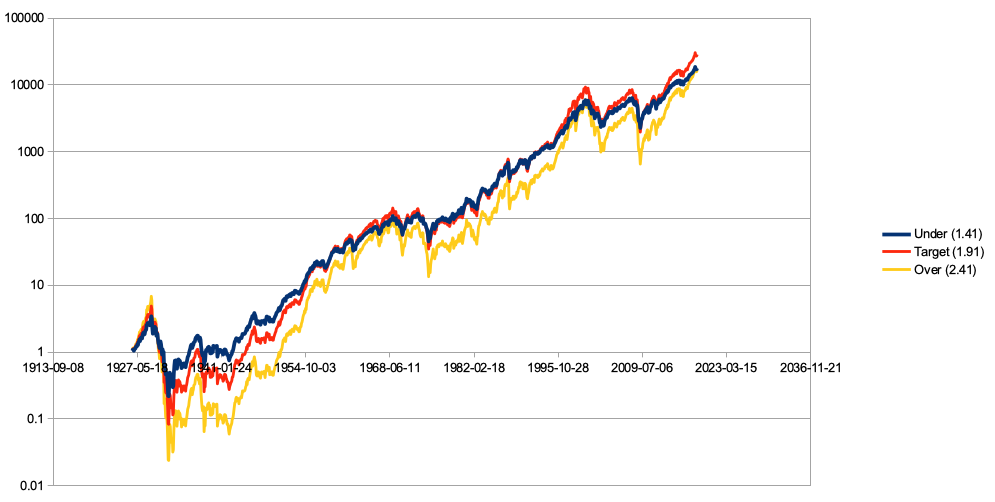
This graph uses a log scale, so a price drop from one horizontal line to the one below represents a 90% drawdown. As we can see, the over-leveraged portfolio experienced multiple 80%+ drawdowns, and went through an extraordinarily painful 99.6% drawdown during the Great Depression. The over-leveraged portfolio underperformed the under-leveraged one throughout almost the entire period, and only made up the difference right at the end of the sample, (as well as surpassing the under-leveraged portfolio for exactly one month at the peak of the tech bubble).

An investor who truly has logarithmic utility doesn’t care about drawdowns. Individuals in practice almost certainly don’t experience logarithmic utility of money—in this simulation, almost every real-world investor would strongly prefer the 1.41-leveraged portfolio over 2.41. But perhaps altruists should bite the bullet on this and accept that the two strategies are equally good for a philanthropically-directed basket of money. I am not convinced that altruists should in fact use a logarithmic utility function, but I find it plausible at least. We have some theoretical reasons to prefer logarithmic utility; for more on this, see Owen Cotton-Barratt’s The Law of Logarithmic Returns. I provide some open-ended (and inconclusive) discussion of this question in a previous essay, under “Risk aversion for altruistic causes”.

But uncorrelated donors are nearly risk-neutral, which suggests such philanthropists (if they exist in practice) might prefer to take on even more leverage, decreasing geometric returns but increasing expected arithmetic returns. Such an investor would knowingly accept a high probability of getting worse performance than the logarithmic-utility investor, in the hope of getting lucky with an unlikely but extremely valuable (to them) market upswing. That sort of strategy would be crazy for most investors, but it might make sense for altruistic portfolios.

Some sample portfolios

Below, I present summary statistics for various portfolios with empirically optimal (“target”) leverage and with 50 percentage points under or over the target. All portfolios assume leverage costs RF + 1%. Observe that exceeding the leverage target for the value/momentum portfolio results in bankruptcy.

In addition to the summary statistics presented previously, these tables include the Ulcer Index, a risk indicator invented by Peter G. Martin that measures the depth and severity of drawdowns.

Table 7: US stocks, 1927-2018

	Lev	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Under	1.41	0.29	11.2	26.0	32.8	94%
Target	1.91	0.23	11.8	35.2	45.7	98%
Over	2.41	0.17	11.2	44.5	57.2	99.6%

Imagine an alternative world where we choose our desired leverage based on the sample period 1952-2018, and then the Great Depression begins in 2029 instead of 1929. Using the methodology above, we choose 2.75 as the point of empirically optimal leverage. Then when the Great Depression hits, the portfolio experiences a 99.9% drawdown during the Depression, but luckily does not go bankrupt. It does not go bust unless we use 3.43:1 leverage or more.

Table 8: 60% US stocks, 40% US bonds, 1947-2018

	Lev	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Under	3.99	0.30	15.8	37.4	38.6	91%
Target	4.49	0.27	16.0	42.1	44.2	94%
Over	4.99	0.24	15.8	46.8	49.7	96%

Table 9: US val/mom, 1952-2018

	Lev	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Under	2.42	0.61	34.5	47.8	35.1	92%
Target	2.92	0.53	36.1	57.7	44.4	96%
Over	3.42	-1.48	-100.0	67.6	486.5	100%

See Appendix B for additional tables.

Rebalance timing luck

Optimal leverage is vulnerable to rebalance timing luck⁹. The performance of a leveraged portfolio might change dramatically if one starts investing a few days earlier or later.

We would like to know how a historical portfolio would change if we put the rebalance date on different days of the month. To test this, I constructed 22 portfolios, each of which rebalances once every 22 trading days, one portfolio for each possible start day. (I use the number 22 because there are approximately 22 trading days per month.) I constructed these portfolios over US equities 1927-2019.

The median portfolio had an empirically optimal leverage of 1.83, but the portfolios ranged from a minimum of 1.63 to a maximum of 1.97.

Table 10: Min/median/max values of summary statistics for the 22 portfolios

	Lev	Sam	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Min	1.63	1.38	0.23	11.0	32.0	41.3	97%
Median	1.83	1.55	0.23	11.2	33.4	44.7	98%
Max	1.97	1.62	0.23	11.7	35.5	46.8	98%

I also tested how the portfolios would have performed if we had gotten “maximally unlucky” and used the highest leverage of 1.97 across all portfolios. Some would have experienced >99% drawdowns, but none would have gone bust.

This shows that even choosing a slightly different rebalance date can non-trivially change the outcome of a portfolio.

Path dependence

In theory, markets follow a random walk: each period’s return is independent of the last. In practice, bad months tend to cluster together, as they did in 1929, 2000, or 2008.

For investors with logarithmic utility, this doesn’t matter. Investors with sub-logarithmic utility prefer bad months to distribute evenly.

We can see the effect of this by taking monthly returns of simulated portfolios and shuffling their order. The shuffled portfolio has all the same moments as the original, but sub-logarithmic utility functions prefer most shuffled portfolios over the original.

Unlike logarithmic utility, someone with sub-logarithmic utility is not indifferent to the sequencing of returns, and we cannot simply look at the total return of a portfolio. One way to express to what extent someone prefers a particular portfolio is to calculate the return of all rolling 5-year periods (or 10-year, or 2-year, or whatever) and find the average utility over all rolling returns, using the isoelastic utility function.

If we do this, we find that portfolios where the returns are randomly re-ordered usually (but not always) produced higher expected utility than the original portfolio. (Results not shown.) This means people with sub-logarithmic utility dislike actual market returns more strongly than the return, standard deviation, skewness, or any other statistical moment might suggest—which means they want to take less leverage than the Samuelson share.

This subject deserves much more detail, but as this essay primarily focuses on logarithmic utility, I will leave it for another time.

How does ex-ante optimal leverage compare to ex-post?

To determine optimal leverage for each portfolio, we looked at the portfolio’s performance at the end of the period and maximized geometric return. But we can’t do that in real life because we don’t know what future returns will look like.

What happens if we calculate optimal leverage ex-ante instead of ex-post?

One naive way to decide how much leverage to use: At each point in time, calculate what the empirically optimal leverage would have been over all previous periods, and use that amount of leverage for the following period. We can do better than this in practice, but let’s start with this method and see what happens.

This method requires limiting our time range—we have to spend some number of years gathering data so we can get an initial estimate of the expected return/standard deviation. For this backtest, I chose 20 years as the waiting period. Because this reduces the sample period by 20 years, it makes the backtest more sensitive to the specific conditions of the tested time range.

Some sample portfolios

Table 11: Ex-ante and ex-post leverage for US stocks, 1947-2018

	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Un-leveraged	0.45	10.8	14.6	12.1	50%
Ex-ante	0.46	14.1	21.2	17.4	61%
Ex-post	0.27	15.1	39.6	42.5	93%

Table 12: Ex-ante and ex-post leverage for 60% US stocks, 40% bonds, 1967-2018

	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Un-leveraged	0.43	9.3	10.1	6.6	30%
Ex-ante	0.28	15.9	38.1	39.1	83%
Ex-post	0.23	13.2	35.6	37.2	86%

Table 13: Ex-ante and ex-post leverage for 60% US value/momentum, 40% bonds, 1972-2018

	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Un-leveraged	0.74	14.4	12.6	6.5	33%
Ex-ante	0.61	37.4	51.7	26.8	81%
Ex-post	0.44	31.1	56.8	37.2	92%

See Appendix C for additional sample portfolios.

Commentary

None of these portfolio constructions show a large difference between the CAGRs of the ex-ante and ex-post portfolios. In fact, the ex-ante portfolios have a higher CAGR in two out of three samples, and a higher Sharpe ratio in all three. I was actually surprised by this result—I don’t know how to explain this and I’m inclined to attribute it to coincidence. Importantly, this suggests that choosing Samuelson share ex-ante by naively extrapolating past returns might actually not work too badly.

We can probably do better than simply extrapolating past return and standard deviation. Colby Davis’ The Line Between Aggressive and Crazy proposes a methodology for estimating forward-looking return and standard deviation:

• Estimate equity returns using earnings yield.
• Estimate bond returns using the yield to maturity.
• Estimate volatility as the trailing 60-day standard deviation.

His backtest covers a shorter time period (1993-2017), but he does find that over the sample, this methodology substantially outperformed the strategy that uses constant leverage equal to the ex-post optimal Samuelson share¹⁰. Davis writes: “This is because by estimating volatility in real-time, the forward-looking […] investor is able to mitigate some of the worst drawdowns that the constant-leverage investor dealt with.”

This methodology does require more rebalancing because it changes the leverage target every time volatility changes, which will incur greater transaction costs. This does not matter much for a portfolio that invests in highly liquid index funds, but it may pose issues for the concentrated value/momentum and TSMOM portfolios (or other concentrated portfolios).

Conclusions

According to the standard theoretical model of asset returns, the Samuelson share tells us how much leverage to use. We began by considering some caveats that might make portfolio behavior in practice look worse than the theoretical model suggests:

• Mean reversion
• Left skew of investment returns
• Unpredictability of future returns
• Cost of leverage
• Transaction costs
• Taxes
• Portfolios can’t be adjusted continuously

We looked at some simulated historical portfolios and saw that the Samuelson share usually did not differ much from empirically optimal leverage, with or without accounting for the cost of leverage and transaction costs. This suggests that, for the tested portfolios, mean reversion, left skew, and non-continuous rebalancing did not much affect optimal leverage. However, we saw that using too much leverage can potentially result in bankruptcy, which suggests we should use caution and probably should prefer to under-estimate leverage rather than over-estimate it.

Perhaps the most important caveat to the theoretical model is the unpredictability of future return. We attempted to get a sense of how this matters by looking at what would have happened in historical portfolios if we had used too little or too much leverage. We saw that the “under” and “over” portfolios usually had the same geometric return, but that the “over” portfolio sometimes lost all of its money. This result again suggests that an investor who wishes to maximize geometric return should still prefer not to use enough leverage than to use too much.

The portfolio simulations explicitly accounted for costs of leverage and transaction costs. According to these simulations, these costs do reduce optimal leverage, but this can be accounted for by subtracting costs from the expected return when calculating the Samuelson share. Of course, this requires that we accurately estimate costs, which we cannot do perfectly. But we can estimate costs more reliably than future portfolio return and volatility.

The final remaining caveat, taxes, was not considered. This caveat does not apply to all investors. Foundations do not pay taxes on capital gains, and individuals can invest tax-free using a donor-advised fund. Investors in the United States can avoid capital gains taxes on their non-charitable funds with a 401(k) or an IRA.

For investors who must pay capital gains tax but can also deduct capital losses, taxes reduce both expected return and standard deviation by the same amount. Thus, investors can calculate the tax-adjusted Samuelson share by reducing return \(\mu\) and standard deviation \(\sigma\) according to the tax rate, while keeping the cost of leverage \(R\) unchanged. This will decrease the Samuelson share somewhat, and reduce the return of the leveraged portfolio by somewhat more. Taxes do not change the difference between the Samuelson share and optimal leverage because they scale the returns of the portfolio without changing the shape of the distribution.

Markets are anti-inductive. Just because they behaved a certain way in the past does not mean they will continue to behave that way. So all this analysis on historical data might not apply to markets in the future. That said, the high-level insights drawn did not depend on any assumptions that contradict the efficient market hypothesis, so I have no particular reason not to expect the insights to continue to apply. Rather, I would simply be cautious about making overly strong assumptions about future market behavior. We can draw some interesting conclusions, but hold them weakly.

All things considered, halving the Samuelson share—the plan I discussed previously—appears too conservative. But simply using the Samuelson share unaltered is probably too aggressive. According to the parameters discussed in this essay (e.g., logarithmic utility), forward-looking optimal leverage appears to lie somewhere in between 0.5x and 1x the Samuelson share.

Thanks to Kit Harris for providing feedback on this essay.

Appendix

Appendix A: More sample portfolios

Just within the constraints of my backtest, we can vary portfolios based on which asset classes we include, the proportions of asset classes within a portfolio, fees, and costs of leverage. In the main essay, I only presented a few of the most significant variations. This section provides some hypothetical results for a wider variety of portfolios.

In addition to the summary statistics presented previously, these tables include the Ulcer Index, a risk indicator invented by Peter G. Martin that measures the depth and severity of drawdowns.

All of these backtests assume no fees .

(I realize these tables are going past the margins on the page, but there’s not much I can do about it without substantially redesigning my website’s CSS. Apologies to mobile viewers.)

1952-2018, including US stocks, US value/momentum, bonds, and commodities. Cost of leverage equals RF.

	Lev	Sam	Sharpe	CAGR	Stdev	Ulcer	MaxDD	Lev-Sam
US stocks	2.98	3.03	0.28	17.2	43.7	46.0	95%	-0.05
bonds	3.21	2.64	0.12	7.1	23.6	20.8	75%	0.57
commodities	2.43	1.97	0.17	10.0	32.5	40.2	90%	0.46
US val/mom	3.00	3.94	0.56	38.7	59.3	44.8	96%	-0.94
60% US stock, 40% bond	5.17	5.36	0.30	19.7	49.0	47.9	96%	-0.19
60% US val/mom, 40% bond	5.32	6.99	0.58	43.4	64.4	45.5	98%	-1.67
40% US stock, 40% bond, 20% commodities	6.85	7.94	0.36	23.4	50.7	36.2	96%	-1.09
40% US val/mom, 40% bond, 20% commodities	6.71	9.70	0.63	44.2	60.8	38.9	99%	-2.99

1985-2018, including US stocks, US value/momentum, and TSMOM. Cost of leverage equals RF.

	Lev	Sam	Sharpe	CAGR	Stdev	Ulcer	MaxDD	Lev-Sam
US stocks	2.99	3.37	0.33	19.0	45.0	48.2	95%	-0.38
US val/mom	2.72	3.50	0.49	30.3	53.6	39.9	94%	-0.78
TSMOM	8.10	9.58	0.90	95.4	98.9	49.8	91%	-1.48
50% US val/mom, 50% TSMOM	4.69	10.90	1.13	67.1	54.5	35.7	93%	-6.21

1990-2018, including US stocks and international stocks. Cost of leverage equals RF + 1%.

	Lev	Sam	Sharpe	CAGR	Stdev	Ulcer	MaxDD
US stocks	2.94	2.94	0.29	15.6	42.7	50.8	95%
int’l stocks	1.15	0.70	0.15	5.6	18.9	21.3	62%
50% US stocks, 50% int’l stocks	2.24	2.01	0.22	10.0	32.3	36.4	85%

1927-2018, including US stocks and commodities. Cost of leverage equals RF + 1%.

	Lev	Sam	Sharpe	CAGR	Stdev	Ulcer	MaxDD	Lev-Sam
US stocks	1.91	1.60	0.23	11.8	35.2	45.7	98%	0.31
commodities	1.53	1.03	0.16	7.5	24.5	37.9	93%	0.5
66% US stock, 33% commodities	2.52	2.30	0.25	12.8	37.1	45.6	99%	0.22

1927-2018, including US stocks and commodities. Cost of leverage equals RF.

	Lev	Sam	Sharpe	CAGR	Stdev	Ulcer	MaxDD	Lev-Sam
US stocks	2.14	1.89	0.24	13.0	39.5	49.3	99%	0.25
commodities	1.93	1.42	0.15	8.3	30.9	45.0	97%	0.51
66% US stock, 33% commodities	2.86	2.76	0.26	14.7	42.2	48.5	100%	0.1

Appendix B: More over- or under-leveraged sample portfolios

Commodities, 1927-2018.

	Lev	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Under	1.03	0.22	7.1	16.5	25.5	80%
Target	1.53	0.16	7.5	24.5	37.9	93%
Over	2.03	0.11	7.1	32.5	48.2	98%

50% US value/momentum, 50% TSMOM, 1985-2018.

	Lev	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Under	3.83	0.67	34.0	44.5	32.3	78%
Target	4.33	0.61	35.0	50.3	39.5	88%
Over	4.83	0.47	31.4	56.1	50.2	98%

Appendix C: More ex-ante optimal leverage portfolios

All portfolios wait for 20 years before investing, and then estimate optimal leverage at each period by calculating the empirical optimal leverage over all prior periods.

Commodities, 1947-2018.

	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Un-leveraged	0.31	8.5	14.0	15.5	51%
Ex-ante	0.23	8.6	19.4	19.9	55%
Ex-post	0.19	10.0	30.5	37.5	87%

US value/momentum, 1972-2018.

	Sharpe	CAGR	Stdev	Ulcer	MaxDD
Un-leveraged	0.68	17.8	19.5	11.9	57%
Ex-ante	0.75	28.4	31.1	15.1	55%
Ex-post	0.46	28.6	51.8	38.9	94%

Notes