Last updated 2022-04-29.

Confidence: Highly likely.

Some people hold most or all of their wealth in a single asset. A few examples of common situations where people do this:

• Alice works at Google. A large chunk of her compensation comes in the form of Google stock.
• Bob bought bitcoin a few years ago and the price went up a lot. Now, bitcoin accounts for 50% of his net worth.
• Carol used her retirement money to buy a second house, and she earns income by renting it out.

This is usually a bad idea, and you should go to great lengths to avoid it. It’s bad even if you have high risk tolerance, because you can get a better expected return by building a diversified portfolio and then adding leverage.

Key points

• On average, an individual stock provides the same expected return as the total stock market, but with 2-3 times as much risk. You could apply leverage to a total stock market index and get 2-3 times the expected return for the same level of risk as an individual stock. Or you could add leverage to the global market portfolio and get 3-4 times the expected return. [More]
• The same principle applies to other types of individual assets, such as private company stock, rental properties, and cryptocurrency. [More]
• If you hold a lot of money in a single asset and want to diversify, you may have to pay capital gains tax when you sell. The diversification benefits probably overcome the tax hit after about 3-10 years. [More]
• You can reduce taxes by donating to charity, or by putting the money in a donor-advised fund or a foundation. [More]
• If you’re a major stakeholder in an asset, you might depress the price by selling. You can reduce your market impact by selling slowly, or by paying your broker to manage the sale for you. [More]
• An exception: Altruistic investors don’t just care about their own investments, but about the overall altruistic portfolio. If you hold an individual asset that other altruists can’t hold, such as equity in a private company, it might make sense to keep it. [More]
• If the effective altruism community holds on the order of $30 billion in overly concentrated investments, then diversifying these funds could be worth as much as $1 billion in additional donations per year. [More]

Note: In this essay, I make some illustrations using historical market data. Future market behavior will probably look different, so the exact numbers I use won’t apply. But I expect the basic principles to remain true in the future.

Disclaimer: I am not an investment advisor and this should not be taken as investment advice.

Cross-posted to the Effective Altruism Forum.

Contents

• Key points
• Contents
• A primer on risk
• How risky are individual stocks?
  • Assets other than stocks
• The impact of taxes
  • Reducing taxes by donating
• Major stakeholders care about market impact
• Possible exceptions
• Expected value of diversifying
• Acknowledgements
• Changelog
• Notes

A primer on risk

All else equal, investors prefer to reduce risk. We normally measure risk in terms of standard deviation: if asset A has twice the standard deviation of asset B, then A is twice as risky.¹

An investor who wants to increase risk can apply leverage: borrowing money to invest. This amplifies the expected return and standard deviation of their portfolio. Specifically, both quantities increase in proportion to the amount of leverage used.² For example, using 3:1 leverage—borrowing money until you have 3x as much as you started with—would triple the expected return (minus the cost of leverage) and triple the standard deviation.

If we can freely use leverage,³ we don’t care about an asset’s return or standard deviation. What we care about is the Sharpe ratio: the expected return minus the risk-free rate, divided by the standard deviation. If we want to take on greater risk, we can add leverage to increase both the return and the volatility. If we think our portfolio is too risky, we can mix in some T-bills. Either way, the Sharpe ratio stays the same.⁴

Therefore, when comparing investment choices, we should focus on the Sharpe ratios. In theory, we should invest in whatever portfolio has the highest Sharpe ratio, and then add leverage or mix in T-bills to hit the desired level of risk (although we can’t always do this due to practical constraints). As we will see in the next two sections, we can expect a well-diversified global portfolio to provide a higher Sharpe ratio than almost any individual asset.

How risky are individual stocks?

I couldn’t find any published research on the standard deviations of individual stocks. So I did my own analysis.

Using the Center for Research in Security Prices (CRSP) data set, I calculated the month-to-month standard deviation of every US stock from 1960 to 2015.

I divided stocks into categories by market capitalization, and calculated the average stock’s standard deviation within each category. I defined the categories as follows:

• Micro-caps: smallest 40% of stocks
• Small-caps: 40th to 70th percentile
• Mid-caps: 70th to 90th percentile
• Large-caps: 90th to 99th percentile
• Mega-caps: 99th percentile and above

This table gives the average volatility of stocks within each category, and the market cap of the smallest stock in the category as of 2015.

	Standard Deviation	Min Size
Micro	64%	$05
Small	48%	$310M
Mid	42%	$1.6B
Large	40%	$8.3B
Mega	27%	$75B

This graph shows the standard deviation by market cap of stocks from 1995 to 2015:⁶

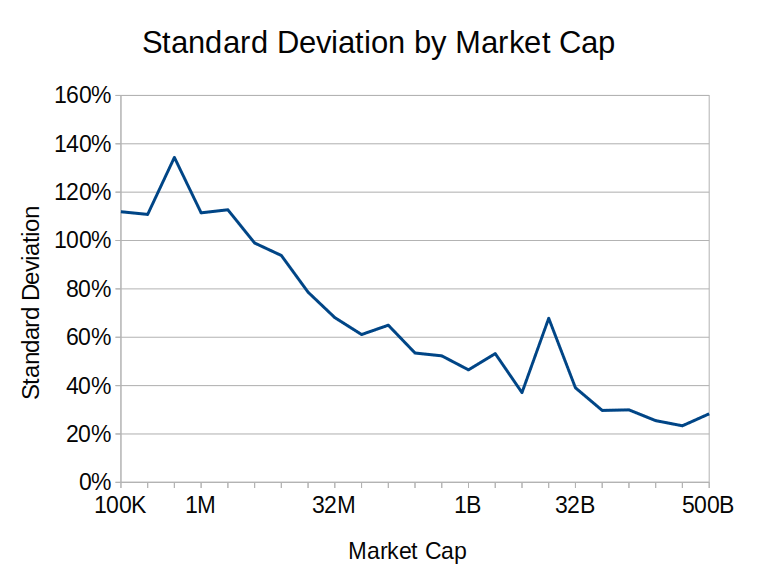
The US stock market has historically had a standard deviation of about 16%. By comparing to the data above, we can see that large-cap stocks experienced about double the volatility of the total market, and small-caps had triple the volatility. Mega-caps were more stable than other stocks, but still showed greater volatility than the total market.

We can corroborate this finding by looking at CBOE volatility indexes. These provide the market’s best guess as to the future volatility of various assets. The VIX gives the projected volatility of the S&P 500; VXAZN, VXAPL, VXGS, VXGOG, and VXIBM project the volatilities of five select stocks (Amazon, Apple, Goldman Sachs, Google, and IBM, respectively). The exact relationships vary over time, but usually, the individual-stock volatility indexes are about twice as high as the VIX.

So far, we’ve seen that the US stock market as a whole is much less volatile than an individual stock. But it’s usually not a good idea to invest only in US stocks. We can reduce volatility even lower by investing in the global market portfolio (GMP). How does individual-stock volatility compare to the GMP?

We can compare the US stock market to a fully diversified portfolio using data from Meb Faber’s book, Global Asset Allocation. The book reports performance from 1973 to 2013:

	T-Bills	US Large-Cap	GMP
Return	5.3%	10.2%	9.9%
Standard Deviation	1.0%	15.6%	8.5%
Sharpe Ratio	0	0.32	0.55

US large-cap stocks (think the S&P 500) had a Sharpe ratio of 0.32. The global market portfolio—which includes global stocks, bonds, and real assets—had a Sharpe ratio nearly twice as high, at 0.55.⁷ Putting this together with the data on individual-stock volatility tells us that individual large-cap stocks were three to four times as risky as GMP, without a meaningfully higher return to compensate. Small-cap stocks were even riskier, although small-caps also tended to earn higher returns, so they had comparable Sharpe ratios to large-caps.

Individual large-cap stocks on average had only 1/3 the Sharpe ratio of the GMP. What does that mean in practical terms?

Suppose it’s 1973, and you’re comfortable with a lot of risk—your target is a 30% standard deviation. You could put all your money in a single stock (like Exxon or IBM) and earn a 10% average return over the next 40 years. Or you could buy the GMP, lever it up 3:1, and earn 19% after fees.⁸ If you invest $100 in the single stock, you will have $4,500 by the end of 2013.⁹ That same $100 in the global market portfolio will turn into $114,000.

Assets other than stocks

The same basic principle applies for single assets other than publicly-traded stock, such as houses, cryptocurrencies, or private equity. Individual assets are far more volatile than the global market portfolio.¹⁰

We don’t really know how volatile individual house prices are, because most houses only get bought or sold once every few years. There’s mixed evidence on how well the aggregate real estate market performs compared to the stock market, but my best guess is real estate performs as well or worse than equities after adjusting for risk. And buying a single property brings idiosyncratic risks, such as property damage or changes in demand in that particular city (or even neighborhood).

(This is not to say it’s a bad idea to buy a house if you want to live in it. I’m specifically talking about buying real estate as an investment.)

We do know how volatile cryptocurrencies are: they’re a lot more volatile than individual stocks.¹¹ So far, bitcoin has justified its volatility with high returns: from 2012 to the end of 2019, it had a Sharpe ratio of 4.1, far higher than that of the global market portfolio. If you expect it to continue returning an average of 300% per year, as it has since 2012, then it might be a good investment. But that’s a pretty bold expectation, and I wouldn’t count on it.¹²

On the subject of private equity, there’s some evidence that venture capital firms outperform public markets.¹³ But this outperformance comes with greater risk: three quarters of entrepreneurs end up with nothing. After adjusting for risk, startup founders on average earn less than they would at a salaried job.¹⁴

The impact of taxes

Suppose you have a lot of money in a single stock, and you want to diversify. But if you sell, you’ll have to pay tax on the capital gains. How much does that matter?

As of 2020, most people in the United States have to pay 15% tax on capital gains. People in the top tax bracket have to pay 20%. Additionally, you may have to pay more if your state charges capital gains taxes. California residents in the top tax bracket have to pay 13.3% in state capital gains tax, for a total of 33.3%. (Apologies to readers outside the US; I don’t know how your taxes work.)

Let’s compare two hypothetical options:

1. Keep holding the single stock, earning an expected 10% return without paying taxes.
2. Sell the stock, pay capital gains tax, and invest in the global market portfolio with 3:1 leverage.

If you invest for long enough, option 2 will earn enough (in expectation) to overcome the cost of paying taxes. At a 15% tax rate, this only takes 1.9 years (in expectation). At a 33.3% rate, it takes 4.7 years. If you’re a long-term investor, it looks appealing to take the tax hit in exchange for higher expected return.¹⁵

But most people probably don’t want 3:1 leverage. What if you invest at, say, 1.6:1 leverage instead? With that amount of leverage, the global market portfolio historically had about the same volatility as the (unlevered) S&P 500.

Before we can answer which option is better, we have to resolve a problem. The GMP with 1.6:1 leverage has lower risk than a single stock, so just looking at the return doesn’t fully capture why we prefer the GMP. How can we compare them?

The solution is to use certainty-equivalent interest rates. If you want 1.6:1 leverage on the global market portfolio, then your certainty-equivalent interest rate is 9.1% (calculated using historical data from 1973 to 2013).¹⁶ That means you’re indifferent between holding the GMP at 1.6:1 leverage and holding an asset that pays out a guaranteed 9.1% per year—which, at the 1973-2013 average risk-free rate of 5.3%, gives an excess return of 3.8% over the risk-free rate. (The risk-free rate today is much lower, so the forward-looking certainty-equivalent interest rate would be lower, too. The 9.1% figure only applies historically.)

Historically, an individual stock had a certainty-equivalent interest rate of 5.4% (0.1% plus the historical risk-free rate of 5.3%). Therefore, holding the GMP rather than the single stock was as good as a guaranteed 3.7% annual return (= 9.1% – 5.4%, or 3.8% – 0.1% if you exclude the risk-free rate). At a 3.7% interest rate, it takes 4.4 years to make up for a 15% capital gains tax, and 11.1 years to recover from a 33.3% tax. 11.1 years is a long time, but many investors have longer time horizons than that.

Reducing taxes by donating

If you ultimately plan to donate your savings, you can do three main things to reduce your tax burden:

1. Donate your stock immediately instead of selling it.
2. Put your stock in a donor-advised fund (DAF).
3. Set up a foundation.

The first option makes sense if you want to donate now. If you want to donate later rather than now, then it doesn’t work for you. But you might still be able to put your stock in a DAF. You can deduct donations to a DAF, and assets you hold inside a DAF don’t incur capital gains tax. But DAFs have three important downsides:

1. DAFs can only disburse funds to legally registered charities.
2. DAFs charge fees, usually 0.6% per year.
3. DAFs typically only let you invest in a few select mutual funds.

The annual fee means the longer you hold money in a DAF, the more money you lose to the fee. But if you keep your money in a taxable account, you have to pay taxes on dividends, which might cost you more than 0.6% anyway—in which case the DAF performs better by avoiding those taxes.

DAFs usually only allow you to invest in a dozen or so pre-selected mutual funds. You can use the available funds to construct a portfolio of global stocks and bonds, but you might not be able to buy alternative assets like gold. And if you want to do something more sophisticated like leverage or mission hedging, you’re probably out of luck.

If you set up a foundation to hold your money, then the foundation is free to invest however you’d like. But foundations have relatively high fixed costs, so it probably only makes sense to create one if you want to donate a lot of money—perhaps somewhere around $10 million. (I don’t know much about foundations, that’s just my order-of-magnitude guess after reading a few articles about how they work.)

But be aware that US donors can only deduct 30% of their adjusted gross income (AGI) when donating appreciated securities. For example, if your income is $100,000, then you can’t deduct more than $30,000 worth of stock. If you donate more than that (including by putting it in a DAF), then you only get to deduct the first $30,000. Foundations have stricter limits—donors can only deduct 20% of AGI when donating to a foundation. Under some circumstances, it might still make sense to make a non-deductible contribution to a DAF, because any assets inside the DAF will not incur taxes if they gain value.

Much more could be said about how DAFs and foundations work. This section is just meant to provide a starting point. I am by no means an expert on taxes; if you plan on incurring a large capital gain, you should first talk to a tax professional.

Major stakeholders care about market impact

If you’re a major stakeholder in an asset, e.g., if you hold a significant fraction of the stock in a publicly-traded company, then you might not want to sell all your holdings at once. If you try to sell too quickly, that pushes down the price, and you end up selling at a substantial discount. That’s not good.

You can still sell large holdings as long as you’re careful. Most brokerage firms can assist large investors with making transactions (for example, Fidelity’s active trader services). Interactive Brokers has an automated algorithm to do this (called accumulate/distribute); I don’t know much about it personally, but an investment professional I trust told me that it works well.

Investors who want to make their own trades can use a simple approach to reduce their market impact (although this probably isn’t sufficient for truly large transactions):

1. Use limit orders, not market orders.
2. When putting in a sell order, only slightly undercut the current best offer.
3. Be patient. Be willing to wait several days to finish trading.¹⁷

Possible exceptions

In general, it’s not a good idea to hold most of your net worth in a single asset. There is at least one exception: if you’re an altruistic investor and you hold an asset that few other altruists own.

Self-interested people only care about how much money they have, but altruists care about how much money all other (value-aligned) altruists have. As an altruist, rather than focusing on your personal portfolio, you want to optimize the overall altruistic portfolio.

In some situations, it might make sense to hold most of your money in a single asset. For example, if you’re a founder or employee at a small private company, you might be the only value-aligned altruist who can hold equity in that company. In that case, you might prefer to hold on to that equity instead of selling. Even though your personal portfolio is highly concentrated, you’re actually diversifying the overall altruistic portfolio by investing in an asset when nobody else can (as long as your holding doesn’t represent too large a percentage of the altruistic portfolio).

As far as I know, that’s the only situation where concentrating your investments in one asset can actually reduce risk. But there are some other situations where you might be willing to accept concentration risk in exchange for some other benefit. For example:

1. You put most of your wealth in a house because you want to own your own home.
2. You’re the founder of a company, and you want to control a majority of the voting shares.

Sometimes, considerations like these might matter enough to outweigh the extra risk. But people usually underestimate the risk involved in concentrating their wealth, and they should diversify more often than they do.

Expected value of diversifying

The effective altruism community probably has on the order of $30 billion in concentrated investments. If we collectively shifted all this money toward a globally diversified portfolio, historically that would have been worth a certainty-equivalent 3.7% return, or just over $1 billion per year. Of course, these numbers are rough estimates. And a lot of funds are probably concentrated in US equities, which isn’t ideal but still isn’t as bad as holding just a single stock. Ultimately, it seems likely that diversifying the collective effective altruist portfolio could be worth $500 million or more per year in extra donations.

Acknowledgements

Thanks to Peter Hurford, David Reinstein, and Gavin Taylor for reviewing drafts of this essay.

Changelog

2022-04-20:

• Update expected value of diversifying based on how EA funding has grown.
• Improve the standard deviation by market cap chart to be more readable.
• Update footnote to reflect the changes to the aforementioned chart.

2022-04-29: Update “Key points” to reflect the changes from 2022-04-20.

Notes